本文共计1234字,预计阅读时长八分钟
回归算法
一、回归的本质
发现y和x的规律,以预测新情况下的y值
二、回归算法的分类
1. 线性回归(Linear Regression)
1)一元线性回归
• 输入
一元自变量x,一元因变量y
• 回归模型
模型输出:y= wx + b
模型参数:w, b
• 损失函数
对每个样本,预测值y' = wx + b, 误差:ε = y - y'
损失函数,即最小化误差平方和:minΣε=minΣ(wx+b-y)
令导数等于0,求出上式的w, b 即可
2)多元线性回归
• 输入
自变量是一个向量x,因变量数值y
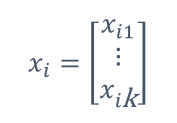
• 回归模型
模型输出:
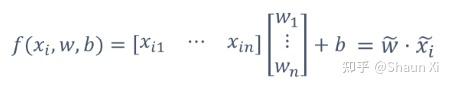
模型参数:w(向量)
• 损失函数
对每个样本,预测值y' = wx , 误差:ε = y - y'
损失函数,即最小化误差平方和:
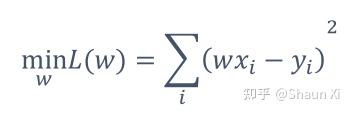
令导数等于0,则
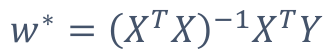
2. 非线性回归(none-Linear Regression)
如果回归模型的因变量是自变量的非一次函数形式,回归规律在图形上表现为形态各异的各种曲线,称为非线性回归。下面主要介绍机器学习中常见的一种非线性回归——逻辑回归(Logistic Regression)
• 输入
自变量x,因变量y
注:y不再是连续值,而是离散值{0,1}
目标:根据特征x,预测发生概率p(y=1|x)和p(y=0|x),哪个概率大,y就取哪个值
• 回归模型
模型输出:此时不能再设y= wx,因为y只能为0或1,所以我们需要换个思路
令:
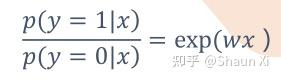
因为左右两边的值域都是 [0,+∞),左边的可以这么理解,
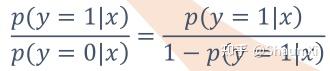
那么,
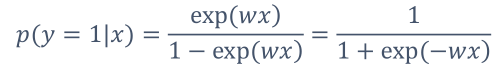
得到形似sigmoid的函数:
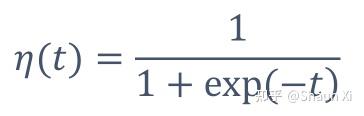
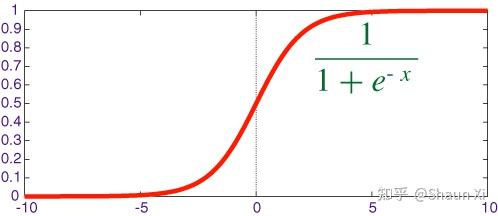
故,将模型设为:
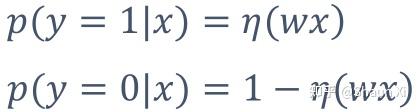
模型的参数:w(向量)
• 损失函数(本篇的精华)
① 因为模型的结果是两个概率,无法计算y的误差。关于概率的问题我们需要换个思路——最大似然估计: 当从模型总体随机抽取n组样本观测后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大。
看不懂对吧?我的理解,就是通过后验概率求先验概率的原理。
一个袋子中有20个球,只有黑白两色,有放回的抽取十次,取出8个黑球和2个白球,计算袋子里有白球黑球各几个。那么我会认为我所抽出的这个样本是被抽取的事件中概率最大的。p(黑球=8)=p* (1-p), 让这个值最大。求导便得到p=0.8,即我们认为袋子中黑球占了80%。
② 最大似然→对数似然:
因为在算法上幂和连乘不好处理(聚合函数里没有连乘,只有连加sum),我们可以加个对数,巧妙地避开了这个麻烦。
③对数似然→负对数似然:
在机器学习需要迭代的算法中,都会有个损失函数,当损失函数小于某个值时,停止迭代,刚才的对数似然是在求最大值,此时加个负号就变成最小值。这样,又巧妙地满足了这个套路。
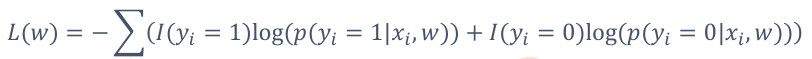
注:这里负对数似然原则上不再叫损失函数,而是有另外一个专有名词——代理函数。
④ 梯度下降法求解:
为了计算得到这个负对数似然函数L(w)的最小值,需要借助梯度下降法
我们可以模拟这样的一个过程:你来到一个盆地,刚好晚上起雾了,能见度很差,如果规定不能坐缆车,只能步行下山,想要尽快到达盆地底部,正常人都会遵循的三个原则:
1.每次选择坡度最陡的方向前进(即梯度的反方向);
2.越接近底部,步频会越小,否则很有可能错过最低点;
3.连续走了几步发现在海拔上并没有太大的变化,基本就可以判断到达了盆地底部。
所以梯度下降法的核心类似:
1.设置初始w,计算L(w)
2.计算梯度d = ▽L(w)
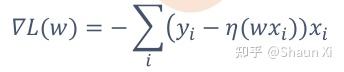
得到下降方向选择:dir = -d
3.调用line search得到下降后的w'和L(w')
i) 设定初始步长c>0,容许度0<b<1,折半因子0<a<1
ii) w' = w+c*dir, 计算得到L(w')
4.迭代与停止条件
i) 令w = w', L(w) = L(w'), c = a*c, 继续第2步;
ii) 如果L(w') - L(w) < b*c,停止(为了避免死循环,设置一个迭代次数k,达到k次也可以停止)。
(个人总结,欢迎指正)

