本文是专栏《Excel必知必会》的第 11 篇教程,如果想了解专栏内容规划,请参阅开篇。
LINEST1. Excel 趋势线类型
1.1 线性趋势线 [Linear]
1.2 指数趋势线[Exponential]
1.3 对数趋势线 [Logarithmic]
1.4 多项式趋势线[Polynomial]
1.5 乘幂趋势线 [Power]
1.6 动态平均值趋势线[Moving average]
2. Excel趋势线的公式
2.1 线性趋势线公式
2.2 指数趋势线公式
2.3 对数趋势线公式
2.4 多项式趋势线公式
(1)二次多项式 (2 阶)
(2)三次多项式 (3 阶)
2.5 乘幂趋势线公式
1. Excel 趋势线类型
添加趋势线时,有 6 种选项,并且可以在 Excel 图表上可以显示趋势线的公式以及 R 平方值。
- 趋势线公式: 最佳拟合曲线的方程式
- R-平方值:代表趋势线的可靠性,愈接近 1 代表拟合程度愈高
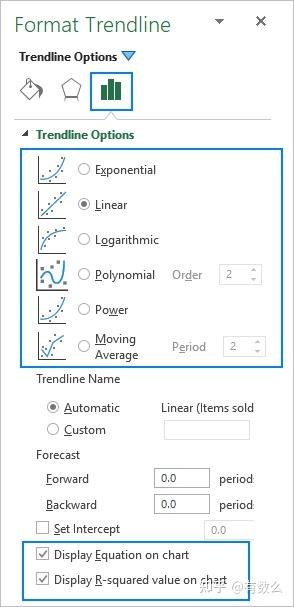
[Linear]当数据在图表中呈现为直线形状,此时可以使用线性趋势线,其经典应用场景是描述随时间持续增长或下降的数据。
如下的线性趋势线展示了销售额在最近 6 个月稳定的增长,其中 \bf{R^2} 为 0.9855 代表当前的线性趋势线对数据拟合程度相当高。
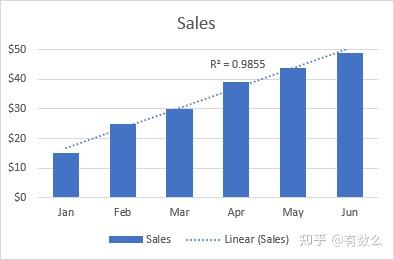
[Exponential]指数趋势线是曲线,揭示数据以增长的变化率进行增长或降低,因此趋势线在数据的首/末端弧度比较高。
指数趋势线在科学中应用广泛,例如人口的增长或者野生动物的减少。
需要注意的是,如果数据中存在负值或零值,无法添加指数趋势线。
如下图表为地球上野生虎的衰减数量。
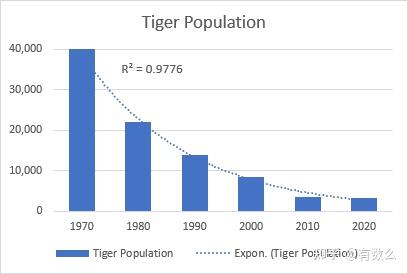
[Logarithmic]当数据曲线呈现快速增长或下降随后趋于平缓,此时可以使用对数趋势线。
适用于对数趋势线的数据既可以为正值也可以为负值。
例如下图,通货膨胀率初始阶段快速升高,一段时间后趋于平稳。
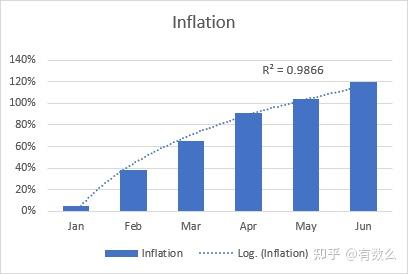
[Polynomial]多项式拟合是一种曲线型趋势线,适用于大量,并且包含多个增长或降落的震荡型数据。
一般来说,多项式的自由度按最大阶乘数进行区分,多项式趋势线的自由度也可以由图上的弯曲数决定。
通常,二次多项式趋势线有一个弯曲(波峰或波谷),三次多项式有1或2个弯曲,四次多项式最多有3个弯曲。
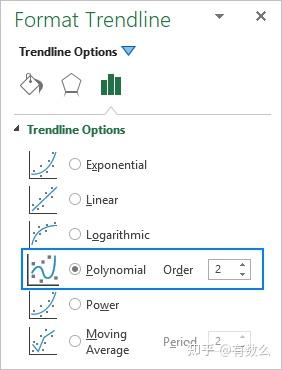
添加多项式趋势线时,通过改变阶数 [Order] 来指定多项式的自由度,默认阶乘为 2。
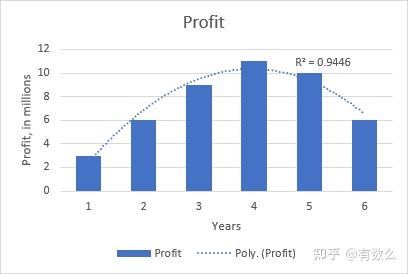
如下图,二次多项式揭示了如下关于产品生命周期以及利润的关系。
前期高利润,中期稳定,后期回落。
[Power]乘幂趋势线与指数趋势线形状相似,但是乘幂趋势线弧线更加对称,常用于以一定增常率增长的数据。
乘幂趋势线不适用于包含负数或零值的数据。
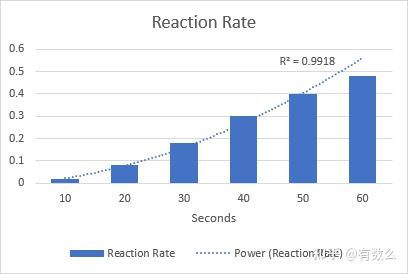
例如说 “化学反应率”乘幂趋势线进行预测。
R 的平方值是 0.9918 说明乘幂趋势线对当前数据拟合完美。
[Moving average]当数据比较震荡存在多个起伏,使用动态平均值可以对一些极端的波动进行平滑处理。
因此,通过在 Excel 动态平均值趋势线指定平滑周期(默认为2)可以对数据进行不同强度的平滑处理。
注意平滑周期设定值越高平滑效果越好,但是同时动态效果会被削弱。
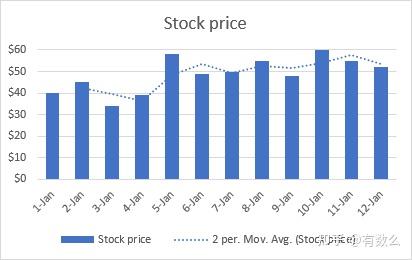
例如使用动态平均值趋势线来观察波动的股价。
2. Excel趋势线的公式
介绍了完趋势线类型以及适用范围,详细讲一讲各类趋势线的公式以及如何使用 Excel LINEST 函数获取趋势线的参数。
Excel 趋势线的公式假定源数据包含两个变量:自变量 x,因变量 y, 通过趋势线公式,对于任意给定的自变量 x 均可以得到预测值 y。
趋势线的公式只能在 XY 散点图上适用,因为只有在散点图中 x,y 轴代表的才是数值数据。
2.1 线性趋势线公式
线性趋势线的公式来源于最小二乘法,关于最小二乘的说明和推导请参阅<<有数么:【EXCEL必知必会】一文搞懂最小二乘法,一元线性回归!>>,这里就不另作解释了。
首先,线性趋势线的公式为:
\bf{ y = a + bx}
这里:
- b 是趋势线的斜率
- a 是线性趋势线的截距
对于线性趋势线,Excel 提供了额外了函数来获取斜率 b 以及截距 a 。
=SLOPE(y,x)=INTERCEPT(y,x)假设自变量 x 的数据区域为 B2:B13 因变量 y 区域为 C2:C13, 函数公式为:
同时也可以使用 LINEST 函数获得趋势线的参数。
CTRL + SHIFT + ENTER如下是使用 Excel 函数获取线性趋势线参数方法对比:
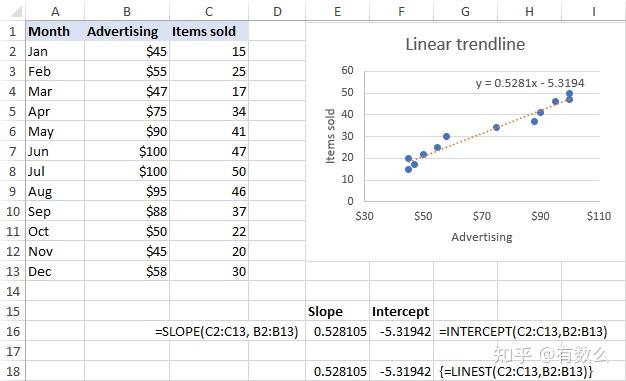
2.2 指数趋势线公式
Excel 中指数趋势线的公式为:
\bf{y = a*e^{bx}}
这里需要确定指数趋势线的参数 a ,b(e 为自然常数 2.7183)
因为 LINEST 函数是对线性回归/趋势线进行求解,对于非线性趋势线,需要转化为线性。
\begin{array}\ & \bf y = a*e^{bx}\\ & \bf \color {blue}{取对数:lny = lna + bx} \\ & \bf 令:y' = lny ; a' = lna\\ & \bf 转化为:y' = a' + bx \end{array}
这样使用可以 LINEST 函数求解参数 a,b:
因此:
=EXP(INDEX(LINEST(LN(y), x), 2))=EXP(INDEX(LINEST(LN(y), x),1,2))=INDEX(LINEST(LN(y), x), 1)对于示例数据:
=EXP(INDEX(LINEST(LN(C2:C13), B2:B13), 1, 2))=INDEX(LINEST(LN(C2:C13), B2:B13), 1)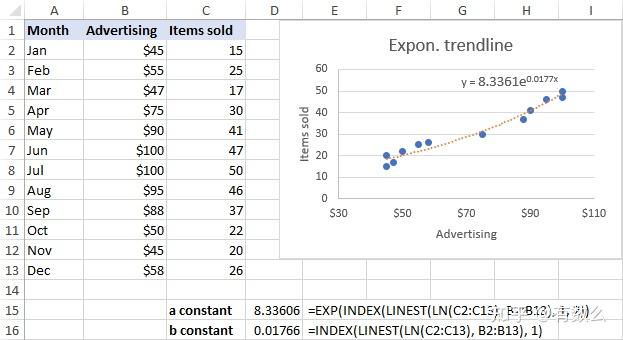
2.3 对数趋势线公式
Excel 中对数趋势线的公式为:
\bf{y = a + b*ln(x)}
同样将对数趋势线转换为线性趋势线后进行求解:
\begin{array}\ & \bf y = a + b*ln(x) \\ & \bf \color {blue} {令:x' = ln(x)}\\ & \bf 转化为:y = a + bx' \end{array}
这样使用可以 LINEST 函数求解参数 a,b:
因此:
=INDEX(LINEST(y, LN(x)), 1)=INDEX(LINEST(y, LN(x)), 1, 2)对于示例数据:
=INDEX(LINEST(C2:C13, LN(B2:B13)), 2)=INDEX(LINEST(C2:C13, LN(B2:B13)), 1)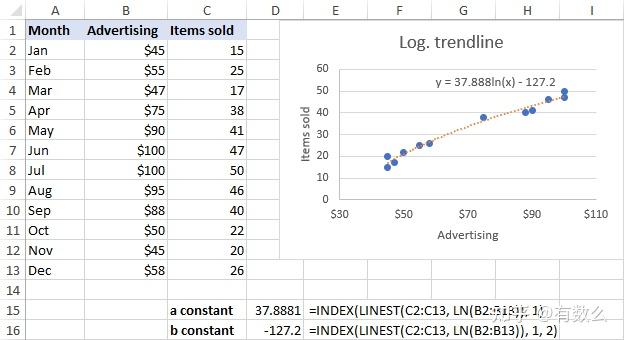
2.4 多项式趋势线公式
Excel 中多项式趋势线的公式为:
\bf y = a + b_1x + b_2x^2 + ... b_6x^6
b_1…b_6 以及 a 是常量
对多项式趋势线参数的求解需要转换为多元线性趋势线
\begin{array}\ & \bf y = a + b_1x + b_2x^2 + ... b_6x^6 \\ & \bf \color {blue} {令:x_2' = x^2, x_3' = x^3 ... x_6' = x^6 }\\ & \bf 转化为:y = a + b_1x + b_2x_2' + ... b_6x_6'\\ \end{array}
取决于多项式的自由度/阶数,可以使用如下函数来获得趋势线参数。
(1)二次多项式 (2 阶)
方程: \bf y =a + b_1x+ b_2x^2
=INDEX(LINEST(y, x^{1,2}), 1)=INDEX(LINEST(y, x^{1,2}), 1, 2)=INDEX(LINEST(y, x^{1,2}), 1, 3)(2)三次多项式 (3 阶)
方程: \bf y =a + b_1x+ b_2x^2 + b_3x^3
=INDEX(LINEST(y, x^{1,2,3}), 1)=INDEX(LINEST(y, x^{1,2,3}), 1, 2)=INDEX(LINEST(y, x^{1,2,3}), 1, 3)=INDEX(LINEST(y, x^{1,2,3}), 1, 4)其他高阶多项式趋势线参数求解方法类似
对于示例数据:
=INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1)=INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 2)=INDEX(LINEST(C2:C13, B2:B13^{1,2}), 1, 3)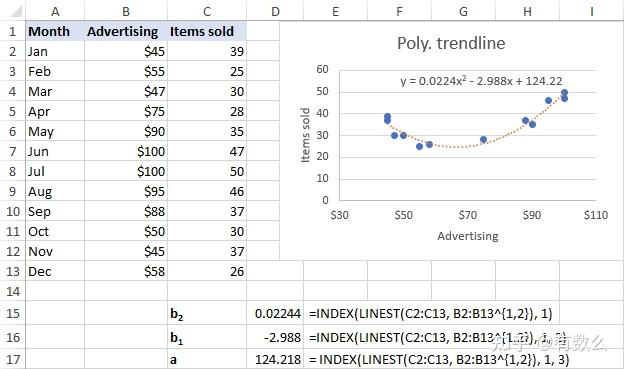
2.5 乘幂趋势线公式
Excel 中乘幂趋势线的公式为:
\bf{y = a * x^b}
对于乘幂趋势线的参数,需要转化为线性趋势线进行求解:
\begin{array}\ & \bf y = a*x^b\\ & \bf \color {blue}{取对数:lny = lna + blnx} \\ & \bf 令:y' = lny ; a' = lna;x' = lnx\\ & \bf 转化为:y' = a' + bx' \end{array}
这样使用可以 LINEST 函数求解参数 a,b:
因此:
=EXP(INDEX(LINEST(LN(y), LN(x)), 2))=INDEX(LINEST(LN(y), LN(x)), 1)对于示例数据:
=EXP(INDEX(LINEST(LN(C2:C13), LN(B2:B13)), 2))=INDEX(LINEST(LN(C2:C13), LN(B2:B13)), 1)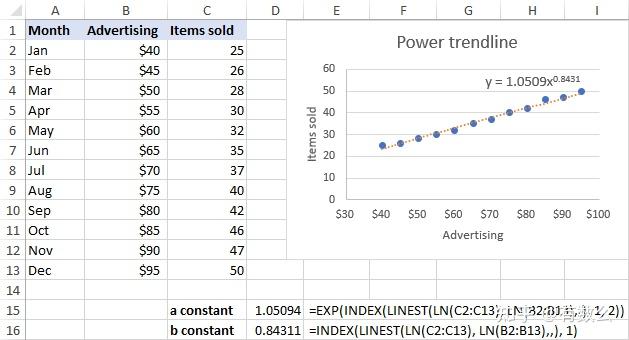
正文结束
参考文档:
传送门:链接:https://pan.baidu.com/s/148zv4mapIrbzCr9r3BT5XA 密码:hji5
最后,每一次点赞、收藏、评论、转载都是对创作最大的鼓励 ❤️

